An Analysis of Cosmic Lucky Prize
It's Phainonomics!
Feb 01, 2025
What’s the best way to simultaneously get millions of weebs excited to play a gacha game AND to also motivate a tired guy to revive his blog for the nth time in his life?
A lottery it seems.
One of the games I play, Honkai Star Rail, is currently running an event titled Cosmic Lucky Prize. While most HSR events feature minigames, puzzles, or even full-blown side stories, Cosmic Lucky Prize is weird in that it offers nearly no gameplay at all! Instead, every day for 7 days, players will be given two choices: gamble or don’t gamble. Don’t gamble and you get a flat 100 jades, but gamble, and you could win a whopping 500,000 jades! Enough to roll gacha 3125 times!
While Cosmic Lucky Prize appears deceptively simple on the surface, a closer look at the event and its rules reveals a rather interesting problem of risk and reward underneath its veil of riches and fortune.
The Game and its Rules
In order to analyze this game, one must first know how it works. Cosmic Lucky Prize’s rules are quite straightforward. A drawing happens every day for 7 days. In each drawing, players can choose to either gamble or bail.
If a player gambles, they enter the pool of all other gamblers. From the pool, a limited number of participants are first selected to be Superstars based on a daily quota. The quota allocates 2 players on days 1, 2, and 3; 3 players on days 4, 5, and 6; and 5 players on day 7, adding up to a grand total of 20 Superstars for the entire event. If chosen, Superstars will receive 500,000 jades. They will also become exempt from being chosen as Superstar again.
After Superstars are selected for a given day, the rest of the gambler pool is divided up for first and second prizes. 10% of the pool is chosen for first prize and receives 600 jades while the remaining 90% get second prize and receive 50 jades.
Everyone else who bailed or didn’t participate automatically gets a flat 100 jades.
I’ve pasted the full rules below:
● In phases 1, 2, and 3, there will be 2 Trailblazers per phase who have a chance to become the Lucky Superstar. In phases 4, 5, and 6, there will be 3 Trailblazers per phase who have a chance to become the Lucky Superstar. In phase 7, 5 Trailblazers will have a chance to become the Lucky Superstar.
● In each phase’s lottery, if a Trailblazer participates but does not become the Lucky Superstar, there will be a 10% chance to win the First Prize and a 90% chance to win the Second Prize.
● In each phase, Trailblazers can only win one of the following: Lucky Superstar, First Prize, or Second Prize. The rewards cannot overlap.
● Across all 7 phases, a Trailblazer can only become the Lucky Superstar once. The same Trailblazer cannot be selected as the Lucky Superstar multiple times.
Math 7th
When I first heard the rules, some things became immediately obvious. For one, the Superstar prize was virtually unobtainable. One source reports HSR at over 5 million players globally (and I suspect this number is even higher in practice). This means that even if only 1% of the player base gambles in the lottery, the chance of being a Superstar is still orders of magnitude below 1%. The Superstar prize acts more as a marketing scheme than anything to drive player excitement towards the event since your chance of winning 500,000 jades is slim to none.
What ended up being more interesting for me, however, were the mechanics behind first and second prizes. Ignoring the Superstar prize and applying some probability, we can compare the expected number of jades awarded in a single drawing for a player who bails versus a player who gambles.
For a bailing player, there is a 100% chance that they receive 100 jades:
\[\begin{align} & E[X] = 1 * 100 \\ & = 100 \end{align}\]So a bailer gets on average 100 jades per draw.
For a gambling player, there is a 10% chance that they receive 600 jades or a 90% chance that they receive 50:
\[\begin{align} & E[X] = 0.1 * 600 + 0.9 * 50 \\ & = 105 \end{align}\]So a gambler gets on average 105 jades per draw.
Comparing these values alone, it seems like a better bet to always gamble since this will net you slightly more jades in the long run. However, this assumption really only holds when the number of draws is high. Unfortunately, this is not the case for this event; only 7 draws will ever happen.
So how does gambling compare with bailing when we account for the fact that there are only a small number of draws? Let’s instead calculate the winnings and chances for each outcome of a player who always bails versus one who always gambles. Let us call these personas the ColdFeet player and the ReachForTheStars player respectively.
The ColdFeet case is straightforward. There is a 100% chance that the player earns 100 jades every draw. This will net them 700 jades by the end of the event.
\[\begin{align} & p = 1 \\ & v = 7 * 100 = 700 \end{align}\]The mean and standard deviation for this case are pretty straightforward since there is no variation:
| Mean | SD |
|---|---|
| 700 | 0 |
On the other hand, the calculation for the ReachForTheStars player is more complicated since they have a chance of losing the gamble and getting second prize. We can calculate the chances and winnings of all possible outcomes for ReachForTheStars by augmenting on the number of times that the player loses the gamble.
Let’s start by finding the chance and payout if ReachForTheStars gets second prize all 7 days.
\[\begin{align} & p = 0.9^7 = 0.48 \\ & v = 7 * 50 = 350 \end{align}\]What if the ReachForTheStars wins first prize only once? We have to choose one of the days for the gambler to win first prize. This can be done with a combination. After that we have to figure out the chance that they win 1 first prize and 6 second prizes. The calculation is then as follows:
\[\begin{align} & p = 0.9^6 * 0.1^1 * {7 \choose 1} = 0.37 \\ & v = 6 * 50 + 1 * 600 = 900 \end{align}\]We can generalize this for any number of times ReachForTheStars wins first prize. Suppose the number of times they win first is \(t\). The probability and payouts are then:
\[\begin{align} & p(t) = 0.9^{7-t} * 0.1^t * {7 \choose t} \\ & v(t) = (7-t) * 50 + t * 600 \end{align}\]Applying the formula for all possible values of \(t\), we can calculate the distribution of jades won:
| t | Probability | Value |
|---|---|---|
| 0 | 0.48 | 350 |
| 1 | 0.37 | 900 |
| 2 | 0.12 | 1450 |
| 3 | 0.023 | 2000 |
| 4 | 0.0026 | 2550 |
| 5 | 0.00017 | 3100 |
| 6 | 0 | 3650 |
| 7 | 0 | 4200 |
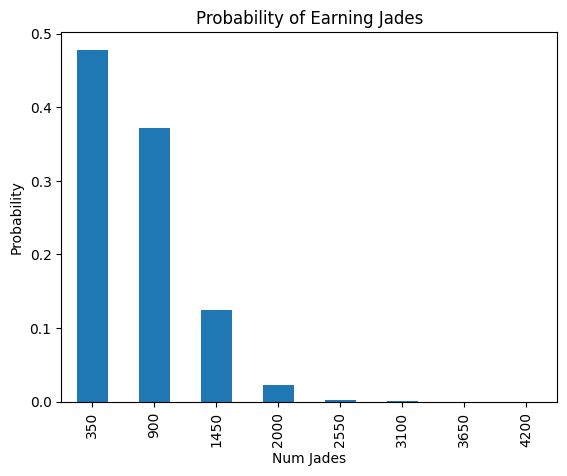
Using some probability formulas that I definitely didn’t need to look up to jog my memory, we can also get the mean and standard deviation of this distribution:
\[\begin{align} & E[X] = \sum_{i} p(x_i) * x_i \\ & Var(X) = E[X^2] - E[X]^2 \\ & SD(X) = \sqrt{Var(X)} \end{align}\]| Mean | SD |
|---|---|
| 735.00 | 436.55 |
As you can see, even with a small number of draws, always gambling still seems to be the better strategy, winning more jades on average than always bailing. Even winning first prize just once will put a ReachForTheStars player ahead of a ColdFeet one by 200 jades.
However, this all comes at the cost of some risk. The chance of winning first at least once is a measly 52%, just over half. Moreover, the effort that ReachForTheStars has to go through is also much higher. They have to have the discipline to log in and choose to gamble every single day of the event.
This led me to my next question: What happens to the other types of players who don’t fall into either of these personas, that is, players who don’t always bail or gamble? Is there a better strategy than always gambling? I didn’t really want to do more math, so it was time to run a little experiment instead!
A Simulated Universe
I ended up writing a simulation to model the Cosmic Lucky Prize lottery. The simulation runs the 7 draws with a population of 5 million. In addition, each of the simulated players acts based on different strategies I think real players will use. The strategies are as follows:
- ColdFeet: Never gambles, always bails. Guaranteed to get 700 jades.
- ReachForTheStars: Always gambles no matter what unless they get Superstar.
- FirstPrizeEnjoyer: Gambles until they win first prize once and then stops gambling.
- Latecomer: Only gambles during the last 4 days. This models players who are either late to the event or get pressured into gambling later because of FOMO.
- Quitter: Always gambles on the 1st day and becomes less likely to gamble with each subsequent day. This models players who lose interest or suddenly get cold feet.
- RandoNoob: Gambles randomly. This models an infrequent and casual player.
After making a few optimizations to my code so that it could scale to 5 million players, I divided the population randomly among the different strategies and ran the simulation.
This is the mean and standard deviation of the jades earned by the entire population after filtering out outliers:
| Mean | SD |
|---|---|
| 696.38 | 287.96 |
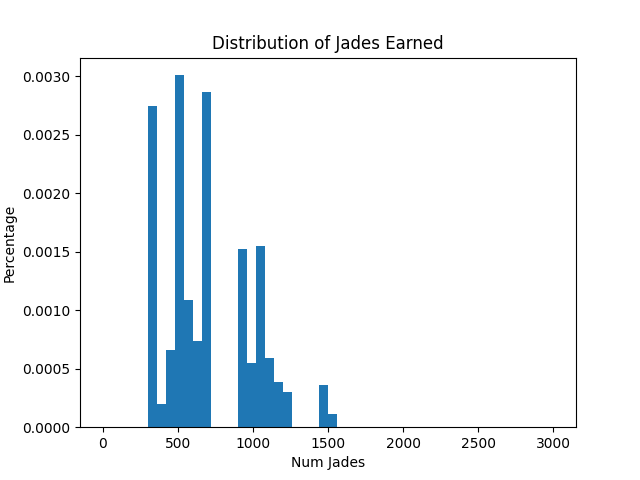
The overall distribution doesn’t tell us much about the strategies though, so I also grouped the data by agent type and ran the same analyses:
| Agent | Mean | SD |
|---|---|---|
| ColdFeetAgent | 700.00 | 0.00 |
| FirstPrizeEnjoyerAgent | 726.10 | 367.11 |
| LatecomerAgent | 669.54 | 253.98 |
| QuitterAgent | 690.06 | 282.22 |
| RandoNoobAgent | 691.40 | 265.69 |
| ReachForTheStarsAgent | 699.57 | 383.16 |
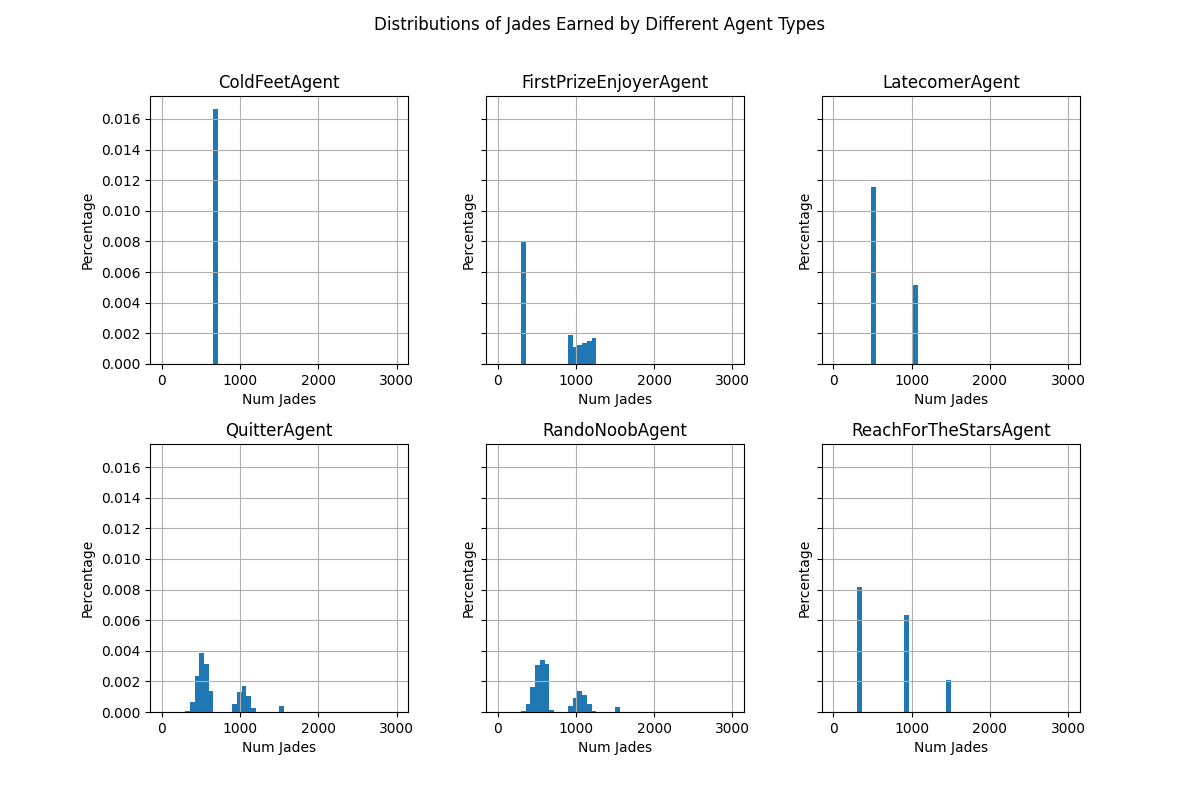
Observations
Taking a look at the distributions, we can see that most of the data is concentrated in small humps throughout the graph, with the humps decreasing in size as the number of jades increases. We see this pattern for both the overall distribution and for the distributions grouped by agent type. These humps seem to represent groups of players who won first prize a certain number of times. Winning first prize would essentially bump a player into the hump for the next bracket up.
Of course, the best performing agents were the ones that could land more reliably in higher bracket humps. Sorting these agents by performance from best to worst, the agents ranked as follows: FirstPrizeEnjoyer, ColdFeet, ReachForTheStars, RandoNoob, Quitter, and finally Latecomer.
Only FirstPrizeEnjoyer, ColdFeet, and ReachForTheStars outperformed the overall average. That being said, both FirstPrizeEnjoyer and ReachForTheStars also had greater standard deviations than the overall standard deviation, indicating higher risk when taking these strategies. ColdFeet was the only strategy beating the overall average that also offered lower risk (since these players obviously never gambled).
One additional observation is that the distributions of Quitter and RandoNoob are very similar in shape. This seems to indicate that quitting early was no different than playing randomly.
Despite the differences in agent performance, the actual outcomes per agent type did not actually seem to be that much different in the grand scheme of things. Even without doing any rigorous comparison of the distributions, it’s pretty clear that all of the agent averages hovered around 700 jades. The standard deviation for even the riskiest strategies only went up to about 400 which means that the vast majority of players were still getting at worst 350 jades and at best around 1100 jades. This kind of makes sense since most of the luckier gambling players likely won first prize once but couldn’t win it more times, landing them into the ~1000 jades earned bracket. Converting to rolls, most players will then earn about 2 to 6 rolls from this event no matter what they do. There is not much of a difference between the min and max of this range to be honest.
Still, if you are someone who wants to make the most out of Cosmic Lucky Prize, you’ll benefit the most if you commit to either being all or nothing. If you missed even a few days and started gambling late, or if you started out gambling but quit later, you end up with a higher chance of receiving fewer jades in the end than if you had just sat out all 7 days instead. Perhaps this is best illustrated in the famous words of a certain senior manager:
“Investing in victory means playing the long game!”
